Story line

Buenos Aires - Conference

You are showing the invitation so that you can enter the conference. There are hundreds of important looking people at the conference. You take a glass of champagne from a tray, and try to look important yourself. After being busy with trying to look important for a few minutes, you approach the person that you are here to get classified information from. He introduces himself as Dr. Nowak Wasilewski. Nowak asks who you are, and if you can prove your knowledge through a test that he has designed by himself.

Challenge: ReadySetAction (crypto)

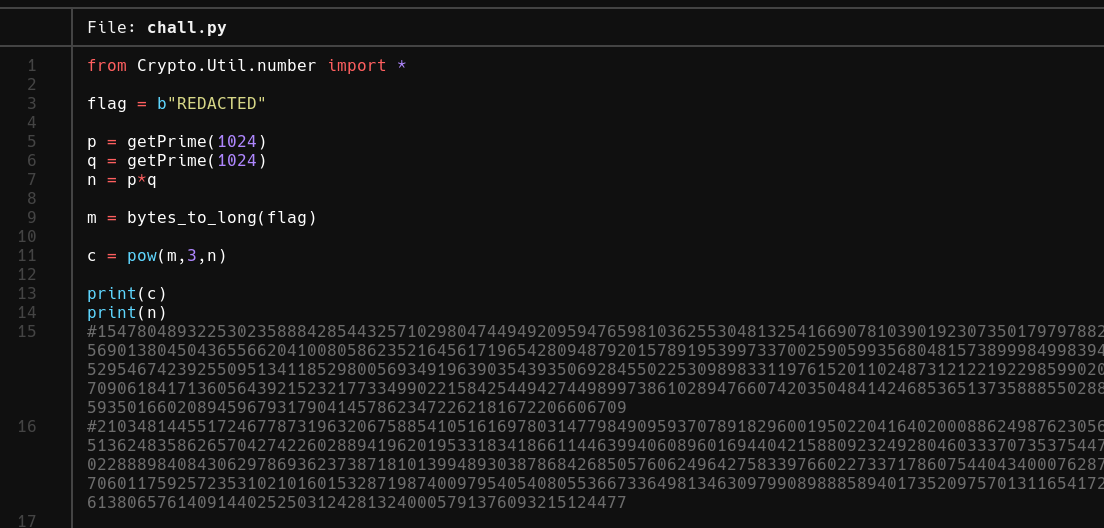
Apparently this script was used to encrypt super secret messages. Maybe there is something interesting in it?

After solving

Nowak is very impressed by your skills. You and him sit down by a table, and you order lots of drinks for him. As the conversation goes on, Nowak begins to loosen up a bit and is talking about all kinds of things. Eventually he accidently reveals the location of an office complex in NYC that seems to have very much to do with the whole operation.

Attachment

attachment.zip

from Crypto.Util.number import *

flag = b"REDACTED"

p = getPrime(1024)
q = getPrime(1024)
n = p*q

m = bytes_to_long(flag)

c = pow(m,3,n)

print(c)
print(n)
#15478048932253023588842854432571029804744949209594765981036255304813254166907810390192307350179797882093083784426352342087386691689161026226569013804504365566204100805862352164561719654280948792015789195399733700259059935680481573899984998394415788262265875692091207614378805150701529546742392550951341185298005693491963903543935069284550225309898331197615201102487312122192298599020216776805409980803971858120342903012970709061841713605643921523217733499022158425449427449899738610289476607420350484142468536513735888550288469210058284022654492024363192602734200593501660208945967931790414578623472262181672206606709
#21034814455172467787319632067588541051616978031477984909593707891829600195022041640200088624987623056713604514239406145871910044808006741636513624835862657042742260288941962019533183418661144639940608960169440421588092324928046033370735375447302576018460809597788053566456538713152022888984084306297869362373871810139948930387868426850576062496427583397660227337178607544043400076287217521751017970956067448273578322298078706011759257235310210160153287198740097954054080553667336498134630979908988858940173520975701311654172499116958019179004876438417238730801165613806576140914402525031242813240005791376093215124477

Recon

The attachment contains two files: chall.py and __pycache__/chall.cpython-39.pyc.

When opening chall.py, we see a script in which a flag is encoded. We also, presumably, see the output of a previous run.

__pycache__/chall.cpython-39.pyc contains the bytecode of a previous run.

Solving

Bytecode

I started out by checking the pycache as this usually isn’t included in the file.

Firsly, I installed pycdc to decompile the bytecode. To do this, run the following command:

pycdc __pycache__/chall.cpython-39.pyc

# Source Generated with Decompyle++
# File: chall.cpython-39.pyc (Python 3.9)

from Crypto.Util.number import *
flag = 'REDACTED'
p = getPrime(1024)
q = getPrime(1024)
n = p * q
m = bytes_to_long(flag)
c = pow(m, 3, n)
print(c)

Unfortunatly, it’s still redacted. Which is a bummer. But otherwise it would also be way too easy for a Google CTF challenge.

Code

So then, let’s move on the chall.py file.

From analysing the code, we can see it firstly gets two random prime numbers using getPrime(1024), and multiplies them.

It then converts the flag to a long.

Afterwards, it wil run pow(m, 3, n). Which is the same as the following:

c =  m ** 3 % n

It will then print c and the product of the two prime numbers.

Let’s start by running the script with “REDACTED” as the flag. To run it, I had to install pycryptodome:

pip install pycryptodome

Then running the script:

python chall.py

208340083409751462917662967455850599109128558322563923008
13613690942133649602062116544305572249357538543629136616006565570128159648146328549284112230115972550824509901897928651857919939814446945134091003675761889274760985268603763526528633214059641383218762734426741922023904934275472430776226339199855092605846993324572692798040926997745203595887220550326802648930725534219128386530143654670295637519434510165129025195704068767045515988758676024370724472946685314139541326829277621885866811911941441787973030331230181454183187506778770932576786354974370048130299280447131529660029449328685936925007328260493634845686069222403477621846404451511286468295329143230842731381879

If we run the script multiple times, we can see that only the lasts value changes. This is expected as n is so big compared to m ** 3 that it will never run the modulo.

Now, let’s start reversing the script.

Reversing

We begin with setting the c and n values, as those are the only ones we know.

c = 15478048932253023588842854432571029804744949209594765981036255304813254166907810390192307350179797882093083784426352342087386691689161026226569013804504365566204100805862352164561719654280948792015789195399733700259059935680481573899984998394415788262265875692091207614378805150701529546742392550951341185298005693491963903543935069284550225309898331197615201102487312122192298599020216776805409980803971858120342903012970709061841713605643921523217733499022158425449427449899738610289476607420350484142468536513735888550288469210058284022654492024363192602734200593501660208945967931790414578623472262181672206606709
n = 21034814455172467787319632067588541051616978031477984909593707891829600195022041640200088624987623056713604514239406145871910044808006741636513624835862657042742260288941962019533183418661144639940608960169440421588092324928046033370735375447302576018460809597788053566456538713152022888984084306297869362373871810139948930387868426850576062496427583397660227337178607544043400076287217521751017970956067448273578322298078706011759257235310210160153287198740097954054080553667336498134630979908988858940173520975701311654172499116958019179004876438417238730801165613806576140914402525031242813240005791376093215124477

Then we have to reverse m. Bruteforcing m here isn’t an option as it would take too long considering its size.

The hard part here is that we have to reverse a modulo which, in principle, is not possible as there are infinitely many numbers that give the same result. For example:

5 mod 3 = 2
8 mod 3 = 2

We can generate these inputs (i.e. 5 and 8) by using the formula d * k + r, where d is de divisor (3), k can be any integer, and r is the remainder (2).

As said above, there are infinitely many inputs for a given divisor and remainder. We can, however, narrow it down a lot, because from bytes_to_long we know that the cube root of the outcome has to be a natural number (i.e. a positive integer).

The boils down to the following equations:

    initial_value ** 3 % divisor = remainder
         divisor * k + remainder = initial_value ** 3
(divisor * k + remainder)**(1/3) = initial_value

Now let’s convert that to code.

For the cube root I’m using iroot from gmpy2 as it supports large numbers, and give an easy boolean value for whether it’s a full number or not. I also stripped down the output as it contained some NULL characters.

from Crypto.Util.number import long_to_bytes
import itertools
from gmpy2 import iroot

remainder = 15478048932253023588842854432571029804744949209594765981036255304813254166907810390192307350179797882093083784426352342087386691689161026226569013804504365566204100805862352164561719654280948792015789195399733700259059935680481573899984998394415788262265875692091207614378805150701529546742392550951341185298005693491963903543935069284550225309898331197615201102487312122192298599020216776805409980803971858120342903012970709061841713605643921523217733499022158425449427449899738610289476607420350484142468536513735888550288469210058284022654492024363192602734200593501660208945967931790414578623472262181672206606709
divider = 21034814455172467787319632067588541051616978031477984909593707891829600195022041640200088624987623056713604514239406145871910044808006741636513624835862657042742260288941962019533183418661144639940608960169440421588092324928046033370735375447302576018460809597788053566456538713152022888984084306297869362373871810139948930387868426850576062496427583397660227337178607544043400076287217521751017970956067448273578322298078706011759257235310210160153287198740097954054080553667336498134630979908988858940173520975701311654172499116958019179004876438417238730801165613806576140914402525031242813240005791376093215124477

for k in itertools.count():
    initial_value, is_exact = iroot(divider * k + remainder, 3)
    if is_exact:
        break

flag = long_to_bytes(initial_value)

flag = flag.replace(b"\x00", b"").decode()

print(flag)

Solution

After executing this code, we get the flag! It’s CTF{34sy_RS4_1s_e4sy_us3}.